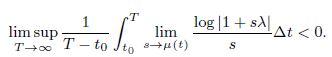REGIONS OF EXPONENTIAL STABILITY FOR HYBRID AND NON-UNIFORMLY SPACED DYNAMICAL SYSTEMS
BILLY JACKSON
DEPARTMENT OF MATHEMATICS
UNIVERSITY OF LOUISVILLE
Abstract. One of the oldest areas of modern mathematics is differential equations. Dating back to the very inception of calculus itself, the study of differential equations has become a cornerstone in applied mathematics. With the 20th Century came the the advance of technology and the the modern age of computing: this advancement also saw the rise in interest of the study of difference equations, long hailed for their ability to numerically investigate their continuous counterparts. The end of the century also saw applied mathematicians beginning to take a keen interest in hybrid dynamical systems: i.e. systems that have both continuous and discrete components. Such systems arise in mathematical ecology quite frequently as many animal, plant and disease populations exhibit behavior that is best modeled hybridly. For example, populations of mosquitoes exhibit continuous growth during late spring and summer and discrete growth during the late fall and winter. Another area of interest occurs in mechanical and electrical engineering, where adaptive control techniques that involve non-uniformly spaced discrete systems often are necessary in the design and implementation of controls for physical systems.
In 1988, a German mathematician named Stefan Hilger developed a framework in his doctoral dissertation that we now call the time scales calculus that both unifies the existing theories of differential and difference equations and extends this theory to other dynamical systems such as the hybrid case of recurring intervals mixed in with isolated points or to the currently popular q-difference equations case. The last 2 decades have seen the application of the theory to control theory as a means for studying and implementing adaptive controls as an alternative to the more classically used optimization methods. This is evidenced by the exponential growth in papers on the topic that have been published by both mathematicians and engineers alike within the last decade alone.
In this talk, I will give a brief overview of Hilger’s framework and discuss more recent developments since his foundational work in the area. Then we will examine a now fundamental result established by Po¨tzsche, Siegmund, and Wirth during their post-doctoral work at Georgia Tech in the early 2000’s. Namely, they showed that a necessary and sufficient condition for the regressive scalar linear ordinary dynamic equation (ODE) defined on a time scale T given by
x∆ = λx, x(t0) = x0
to be uniformly exponentially stable is that
Control theorists have long tried to understand this region that has been very difficult and unwieldy in most cases to compute. I will present recent results that demonstrate a computationally efficient and effective way for computing the stability region SC(T) determined by this inequality in general. We will see that the computation is inherently an ergodic structure: i.e. the global nature of the region is determined by continuous local averages of certain quantities. It turns out that unlike the classical situations when T = R or T = hZ, SC(T) can be disconnected in general. Time permitting, we will conclude by examining a simple bound on the number of simply connected components the region can have by applying a now classical result from Morse in differential topology.